|




 | ||||
|
A Dozen More Arbelos Twinsby Thomas Schoch
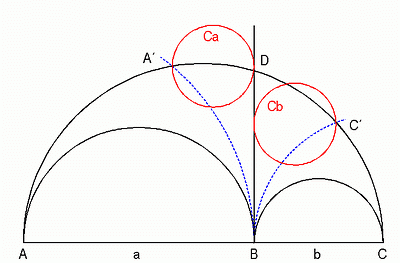
Fig. 1 Draw a circle with radius AB and center at A, crossing arc AC at A', and a second one with radius BC and center at C, crossing arc AC at C'. Let Ca and Cb be the smallest circles touching A' (respectively C') and the line through DB. Both cirles have the same radius as the twins.
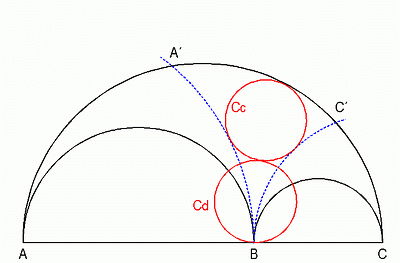
Fig. 2 The circle Cc inscribed into the region bounded by the arcs BA', BC' and A'C' has the same radius as the twins. The smalest circle through B, that touches circle Cc, has the same radius as the twins, too.
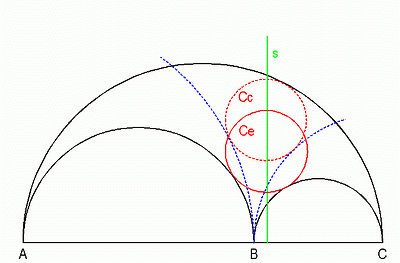
Fig. 3 Draw a line s through the center of circle Cc perpendicular to AC. We will need this special line for some further circles. The circle Ce with center on s, touching semicircles AB and BC, has the same radius as the twins.
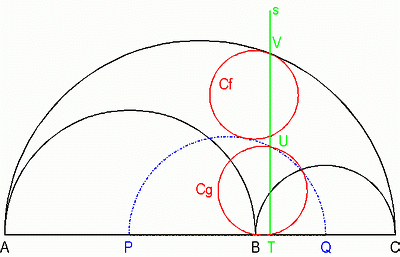
Fig. 4 Let P and Q be the centers of semicircles AB and BC. Draw a semicircle with diameter AC/2 over PQ. Let line s cross this semicircle at U, arc AC at V and line AC at T. The smallest circle Cf through V touching arc PQ has the same radius as the twins. The circle Cg through B, U and T has the same radius as the twins, too.
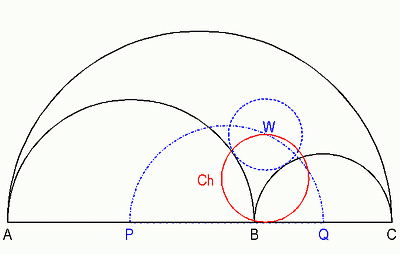
Fig. 5 Draw a circle with center W on arc PQ, touching semicircles AB and BC. The smallest circle Ch, going through W and touching AC, has the same radius as the twins.
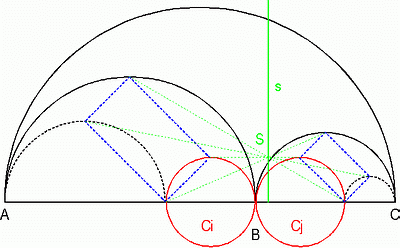
Fig. 6 Draw two smaller Arbeloses, which are geometrically similar to the big one, under the arcs AB and BC. Complete the innermost new semicircles touching B to circles Ci and Cj. Both circles have the same radius as the twins. The rectangles built by the midpoints of the arcs of the smaller Arbeloses and their "B-point" have a symmetrical center S that lies on line s.
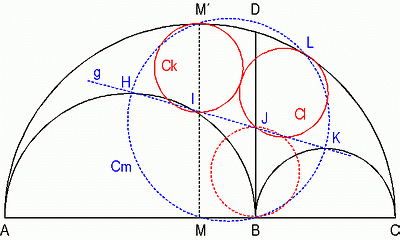
Fig. 7 Draw a line through the midpoint M of AC perpendicular to
AC crossing arc AC at M'. Draw a line g through the midpoints H and K of
arcs AB and BC. This line crosses MM' at I and DB at J. The cirlce through
J touching AC at B is identical to Leon Bankoff's twin (so we don't count
it here). The circle Ck through I, that touches arc AC at M', has the same
radius as the twins. Let Cl be the smallest circle through J, touching arc
AC at L. This circle has the same radius as the twins, too. © 1998 by Thomas Schoch | ||||
|
| |||||